About Infix and Postfix
In an expression if the operators are placed between the operands, it is known as infix notation ( eg A+B) . On the other hand if the operators are placed after the operands then the expression is in postfix notation .( eg AB+)
Infix Notation Postfix Notation
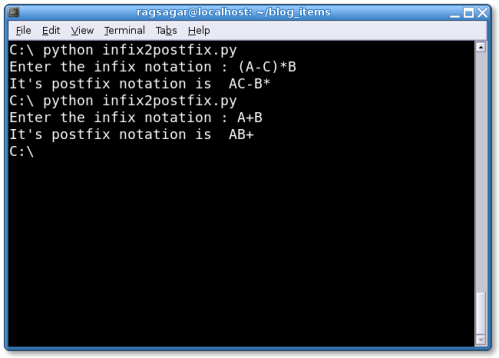
(A-C)*B AC-B*
A+(B*C) ABC*+
(A+B)/(C-D) AB+CD-/
Code
#!/usr/bin/python
#https://ragsagar.wordpress.com
postfix = []
temp = []
operator = -10
operand = -20
leftparentheses = -30
rightparentheses = -40
empty = -50
def precedence(s):
if s is '(':
return 0
elif s is '+' or '-':
return 1
elif s is '*' or '/' or '%':
return 2
else:
return 99
def typeof(s):
if s is '(':
return leftparentheses
elif s is ')':
return rightparentheses
elif s is '+' or s is '-' or s is '*' or s is '%' or s is '/':
return operator
elif s is ' ':
return empty
else :
return operand
infix = raw_input("Enter the infix notation : ")
for i in infix :
type = typeof(i)
if type is leftparentheses :
temp.append(i)
elif type is rightparentheses :
next = temp.pop()
while next is not '(':
postfix.append(next)
next = temp.pop()
elif type is operand:
postfix.append(i)
elif type is operator:
p = precedence(i)
while len(temp) is not 0 and p <= precedence(temp[-1]) :
postfix.append(temp.pop())
temp.append(i)
elif type is empty:
continue
while len(temp) > 0 :
postfix.append(temp.pop())
print "It's postfix notation is ",''.join(postfix)
Code Explanation
Above code converts infix notation in variable infix into postfix notation and stores in postfix list. This algorithm makes use of list temp to hold operators and left parantheses in the infix notation. The postfix list will be constructed from left to right using operands from infix and operators which are removed from temp.